Graphs and Tries – From Connections to Clever Text Searching

Some data structures are just fun to work with—and this post covers two of our favorites: graphs and tries. Graphs let us represent complex, interconnected systems, while Tries enable lightning-fast word lookups, like auto-complete when typing an email.

What is a Graph?

A graph is a data structure made up of:

Nodes (or vertices) – individual entities
Edges – connections between nodes

Types of Graphs

Directed vs Undirected: Are the edges one-way or two-way?
Weighted vs Unweighted: Do the edges have a cost or value?
Cyclic vs Acyclic: Can you loop back to where you started?

Real-World Examples

Social networks – People (nodes) connected by friendships (edges)
Google Maps – Intersections (nodes) connected by roads (edges with distance/time)
Airline routes – Airports connected by direct flights

Graph Algorithms

We’ve already explored how to use graphs to solve powerful problems:

📍 Dijkstra’s Algorithm – Finding the shortest path
🧭 A* Search – Smarter pathfinding using heuristics

Graphs provide the foundation. Algorithms bring them to life.

Tries (Prefix Trees) – One of Our Favorite Structures!

If you’ve ever typed a few letters into a search box and seen suggestions pop up instantly, chances are you’ve interacted with a Trie.

A Trie is a tree-like data structure that stores words by their prefixes. Instead of storing full words in a list, it breaks them into characters and shares common prefixes to save space and speed up lookups.

Real-World Use Case: Email Auto-Complete

When you start typing ja, your email app suggests:

james@...
jane@...
jack@...

A Trie makes this easy by storing all email addresses character by character and navigating down matching paths.

Trie Structure Overview

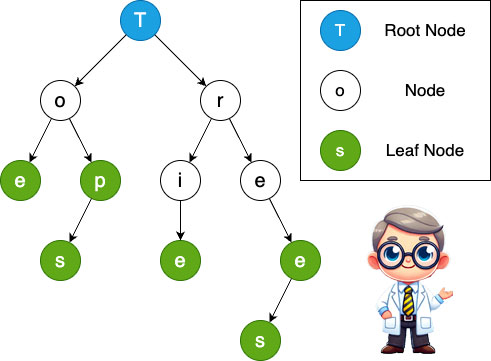
Trie Example

Each node:

Represents one character
Has a map of children
Tracks whether it marks the end of a word

Trie Pseudocode

function insert(word):
    current = root
    for character in word:
        if character not in current.children:
            current.children[character] = new TrieNode()
        current = current.children[character]
    current.is_end_of_word = true

function search(prefix):
    current = root
    for character in prefix:
        if character not in current.children:
            return []
        current = current.children[character]
    return collect_all_words_from(current)

Trie Implementation in C

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>

#define ALPHABET_SIZE 26

typedef struct TrieNode {
    struct TrieNode *children[ALPHABET_SIZE];
    bool is_end_of_word;
} TrieNode;

TrieNode* create_node() {
    TrieNode* node = (TrieNode*) malloc(sizeof(TrieNode));
    node->is_end_of_word = false;
    for (int i = 0; i < ALPHABET_SIZE; i++)
        node->children[i] = NULL;
    return node;
}

void insert(TrieNode* root, const char* word) {
    TrieNode* current = root;
    while (*word) {
        int index = *word - 'a';
        if (!current->children[index])
            current->children[index] = create_node();
        current = current->children[index];
        word++;
    }
    current->is_end_of_word = true;
}

bool search(TrieNode* root, const char* word) {
    TrieNode* current = root;
    while (*word) {
        int index = *word - 'a';
        if (!current->children[index]) return false;
        current = current->children[index];
        word++;
    }
    return current->is_end_of_word;
}

Performance Characteristics

Operation	Time Complexity
Insert a word	O(m)
Search a word	O(m)
Space complexity	O(n * m)

Where:

n is the number of words
m is the average word length

Tries trade space for speed: they use more memory but give blazingly fast lookup times—perfect for autocomplete, spell checkers, and text indexing.

Challenge Time! 🔍

Implement a Trie in your language of choice.
Use it to auto-complete a dictionary of names or cities.
Bonus: Add support for deleting words from the Trie!

Coming up next: Advanced Structures like Bloom Filters and Fenwick Trees – tools that use clever tricks for probabilistic searches and fast numeric operations.